Hello Interactors,
My last post on fractals led me to refamiliarized myself with the man who coined the term, Benoit Mandelbrot, and his influential work on the fractal-like wonders of nature. I didn’t realize he was following in the footsteps of 19th century mathematicians critical of the absolutist purity of Euclidean geometry – themes I recently explored here and here.
My journey led me to a memory of a plane landing on a plane and the complexities that surface on the surface.
Please don’t be shy. Leave a comment or a like. Or just hit reply with a smiley face and a hello!
Now let’s go…
I have a childhood memory, fueled by a crayon drawing, of watching a plane land at the Des Moines airport. My dad was returning home after a business trip. Over time, this memory transformed into a riddle most likely inspired by high school calculus. The riddle posed a question: as the distance between the plane and the runway progressively decreases, when does it equal zero? My pondering was rooted in the observation that, at a microscopic level, the rubber of the tire and the rough surface of the concrete never truly merge into zero. The presence of black streaks on the tarmac from rubber left behind served as evidence. According to classical physics, at an atomic level, the distance between a landing plane and the runway approaches zero but never truly reaches it.
This is because the outermost electron clouds of the atoms in both the tires and the runway surface repel each other due to electromagnetic forces, creating a minute gap between them, measured in angstroms (10 to the power of -10 meters). However, from a practical standpoint, classical mechanics tells us that at a macroscopic level, the plane does make contact with the runway and eventually comes to a stop. Classical mechanics focuses on the behavior of objects on a larger scale, which outweighs the effects observed at the microscopic level. The mechanics of "touchdown" do not rely on atomic physics to achieve zero distance for the safe arrival of our loved ones.
In my childhood crayon drawings, I depicted the runway as a straight line and the plane's wheels as a circle. Yet, this representation itself is a macroscopic interpretation of reality. If we were to examine my marks with a magnifying glass, we would see fragmented wax resting on the textured paper's peaks and valleys rather than perfectly straight lines or round circles. Similarly, we would find fragments of rubber deposited on the peaks and valleys of the concrete runway.

In the realm of high school calculus, the line representing the runway and the circle representing the wheel would be precisely drawn on rigid gridded paper using a plastic flowchart template, akin to the tools my dad used to pseudocode his COBOL programs he no doubt was debugging with his colleagues in Toronto.

Mathematically, I would have described the landing as the height of the plane decreasing as a function of time, incorporating concepts like velocity and acceleration. This interplay between decreasing height and time signifies the plane's motion until it decelerates and reaches a minimum altitude, indicating touchdown. I would have positioned the circle of my plastic template precisely on the flat line, accompanied by an equation describing the moment of touchdown.
However, in 1982, two years before I was in calculus and the year I was learning geometry, mathematician Benoit B. Mandelbrot published "The Fractal Geometry of Nature," a highly influential book. Mandelbrot's work highlighted the importance of mathematics that deviated from the traditional Euclidean curves and shapes. Introduced by ‘modern’ mathematicians like Georg Cantor and Giuseppe Peano a century earlier, the days of regarding mathematics as absolutely pure and unquestioning were being questioned.

Mandelbrot offers why we were set on this smooth, well-worn trajectory of Euclidian mathematical purity,
“The fact that mathematics, viewed by its own creators as ‘absolutely pure,’ should respond so well to the needs of science is striking and surprising but follows a well-worn pattern. That pattern was first set when Johannes Kepler concluded that, to model the path of Mars around the Sun, one must resort to an intellectual plaything of the Greeks–the ellipse. Soon after, Galileo concluded that, to model the fall of bodies toward the Earth, one needs a different curve–a parabola. And he proclaimed that ‘the greatest book [of nature]...is written in mathematical language and the characters are triangles, circles and other geometric figures…without which one wanders in vain through a dark labyrinth.’ In the pithy words of Scottish biologist D’Arcy Thompson: ‘God always geometrizes.’”1
Of the work of Cantor’s set theory and Peano’s space-filling curves, the theoretical physicist and mathematician Freeman J Dyson wrote,
“These new structures were regarded by contemporary mathematicians as ‘pathological.’ They were described as a ‘gallery of monsters,’ kin to the cubist painting and atonal music that were upsetting established standards of taste in the arts at about the same time. The mathematicians who created the monsters regarded them as important in showing that the world of pure mathematics contains a richness of possibilities going far beyond the simple structures that they saw in nature.”2
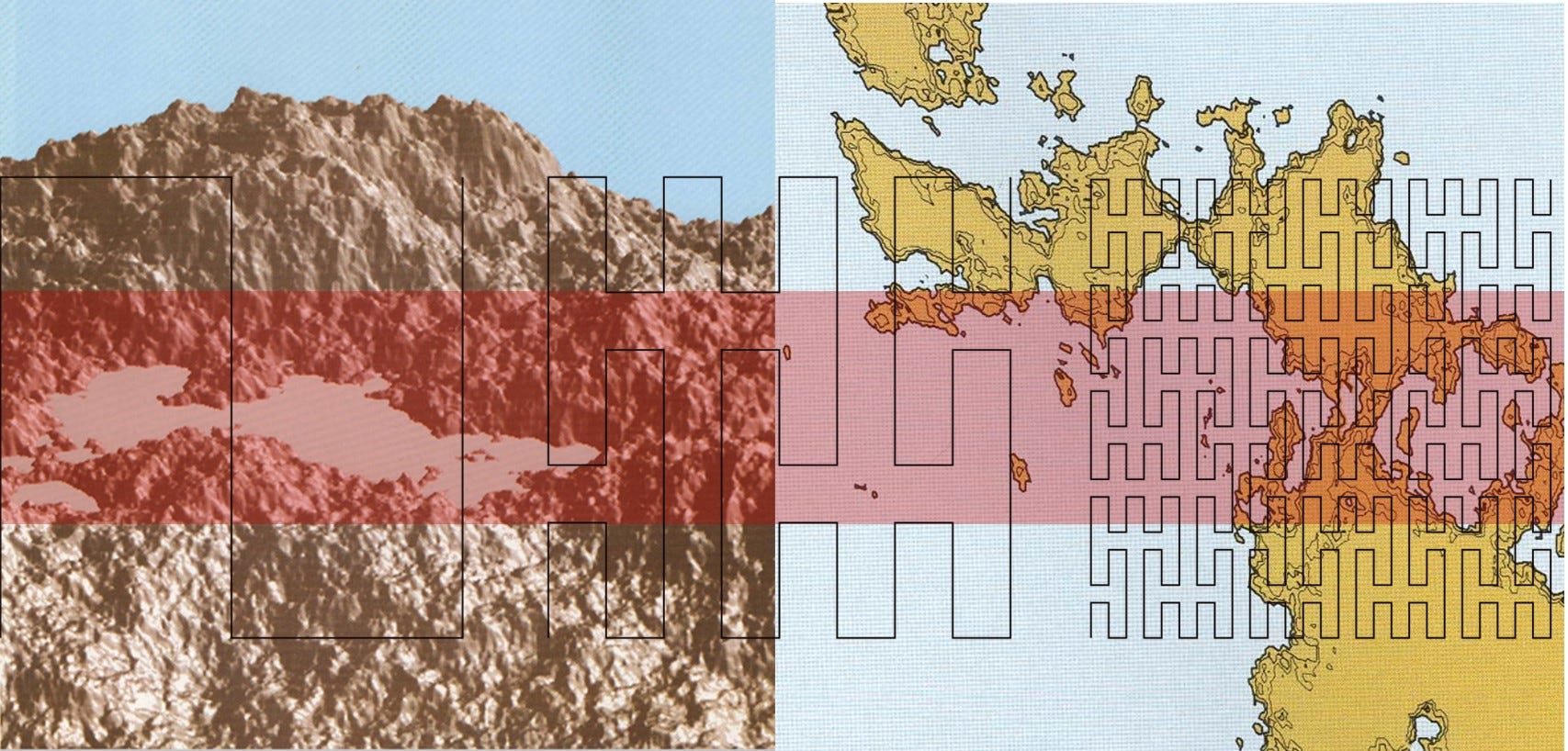
Mandelbrot's research delved into the exploration of fractals, which he described as broken shapes, distinct from the smooth Euclidean curves. These fractals opened new possibilities, allowing for the modeling of complex phenomena found in nature. Mandelbrot's fractal geometry was brought to life through computer-generated images of landscapes and clouds, reflecting the generative algorithms found in nature. These images showcased the jagged, impure, and fractured lines that emerged, challenging the simplicity of Euclidean shapes.

Mandelbrot emphasized that drawing a line between just two points on a square Euclidean plane oversimplifies reality. Instead, he considered the fracturing that occurs when lines connect every point in a square or a cube. In fact, the term "fractal" itself derives from the Latin adjective "fractus," meaning "broken." Mandelbrot highlighted the relevance of fractals lying between the shapes of Euclid, akin to fractions lying between integers.
Mandelbrot offers that
“When mathematicians concluded about a century ago that the seemingly simple and innocuous notion of ‘curve’ hides profound difficulties, they thought they were engaging in unreasonable and unrealistic hairsplitting. They had not determined to look out at the real world to analyze it, but to look in at an ideal in the mind. The theory of fractals shows that they had misled themselves.”3
Mandelbrot's work demonstrated that the seemingly simple crayon drawing of my dad's plane landing concealed profound difficulties. My self-imposed brain teaser was was not an exercise in unreasonable hair-splitting, but rather an analysis of the real world. Fractals, I now know, provide a mathematical framework to quantify irregularities found in natural structures and allow for the analysis and modeling of complex systems exhibiting patterns at different scales.
Mandelbrot's groundbreaking ideas expanded on Cantor and Peano to illuminate the vast possibilities and richness of mathematics beyond the limitations of traditional Euclidean structures. These concepts empower us to better understand the complexities of the natural world and prevent us from being misled by overly idealized notions. Thanks to their work, we are better equipped to explore and comprehend the intricate beauty of the natural world. Even the jagged wax deposits of the line depicting a runway in my childhood drawing.
Mandelbrot, B. B., & Mandelbrot, B. B. (1982). The fractal geometry of nature (Vol. 1). New York: WH freeman.
ibid
ibid